Dr. Robertson's Research
The following links take you to the web pages associated with my research interests.
Photonic Band Structure
Introduction
Photonic band structure refers to the modification of the propagation properties of electromagnetic waves travelling through a periodically modulated dielectric. As an example consider light traveling through a regularly spaced array of spherical glass beads. The effects of scattering and interference of the light by the glass beads clearly would result in a change in the propagation of the waves. The alteration in the propagation properties is particularly significant when the wavelength of the light is approximately equal to the spacing between the beads. In this regime photonic band gaps--frequency intervals in which no photon modes are allowed--can be created for appropriately designed dielectric arrays. The ability to create volumes of space in which no photons of a given band of energies can exist has a number of fundamental and applied consequences. To find out more about the subject you can check out the special issues of the Journal of the Optical Society of America B, Volume 10, 1993 and the Journal of Modern Optics, 41, 1994, or the following internet sites at UCLA, Iowa State University, and Redstone Arsenal.
My current projects in the area of photonic band structure center around two projects. The first is the development and exploration of new analysis tools for calculating the response of Photonic Band Gap Arrays. My particular interest is in the temporal response and I am at present using a time domain simulator based on the transmission line matrix method (TLM) to model electromagnetic wave propagation in dielectric arrays.
Surface Elelctromagnetic Waves on One-Dimensional Photonic Band Gap Materials
The second aspect of my photonic band structure research concerns the use of an attenuated total-internal-reflection (ATR) configuration capable of measuring optical frequency surface electromagnetic wave generation at the surface of photonic crystals. The ATR technique uses a prism in a reflection configuration as shown in the following figure.
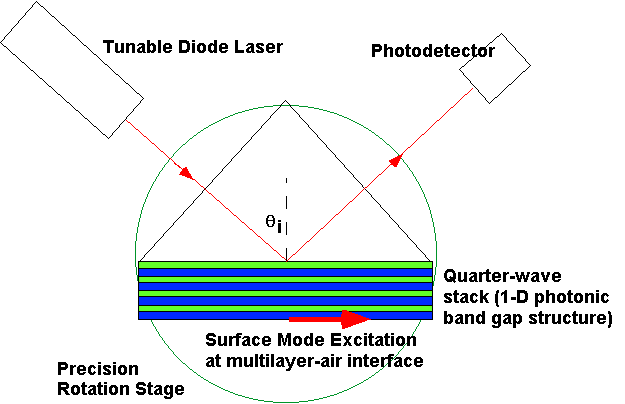
I performed the first experiments that detected surface waves on two-dimensional photonic crystals some years ago [Optics Letters, 18#7, 528-530, 1993.]. Those experiments used the ATR method but they were performed at microwave frequencies for which two- and three-dimensional photonic crystals could be easily fabricated. Making photonic band gap arrays with fundamental gaps at optical frequencies is a current challenge to the field of photonic band gap research, but one that is being met successfully by a number of groups. I hope to have a novel tool for probing these samples as they become available. For now, I use a commercially made Bragg reflector--a one-dimensional photonic band gap material--to verify the performance of the system.
The figure below shows the experimental ATR reflectivity of a Bragg stack at three different wavelengths. For clarity, the curves have been offset vertically.
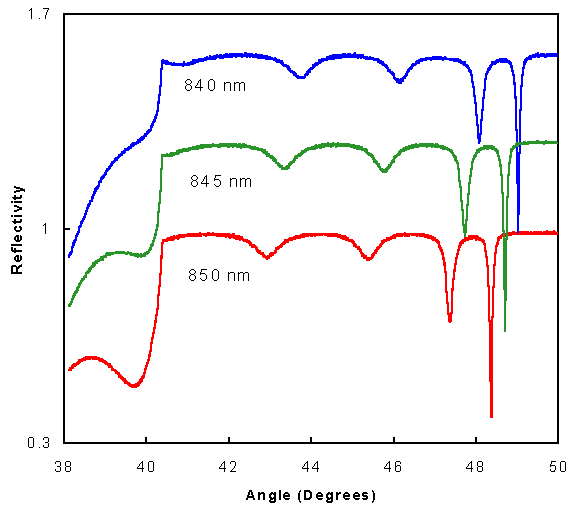
The narrow dip at the highest angle corresponds to the excitation of surface waves at the air/Bragg stack interface, whereas the other dips correspond to lossy modes guided within the multilayer stack. The angular position of the reflectivity minima at each wavelength can be directly related to the wave vector of the corresponding mode. By varying the wavelength of the incident light and finding the corresponding angles of coupling, it is possible to reconstruct the surface wave and guided wave dispersion relations. In principle, the guided mode dispersion should permit one to determine the effective index of the photonic band gap material at the particular wav